数据结构与算法-算法

October 20, 2017 本文总阅读量次 12891

前记

这里是补充数据结构里面缺失的对应算法，略产促

字符串匹配

字符串匹配一般是有一大串字符串target_str, 给给一个待匹配的字符串pattern_str, 找出pattern_str是否在target_str之中, 一般来说target_str会很大而pattern_str会很小.
最简单的就是暴力算法, 然后有Sunday算法和KMP算法, 暴力算法是一个字符一个字符的比较多, 思路简单, 但是计算资源会重复, 而后面两种算法只是基于前面的查找计算资源, 判断是否可以多跳几个字符, 减少计算资源的使用.

朴素的模式匹配算法

假设字母列表长度为m, 想要寻找的长度为n，则从头开始找，到第m-n+1位，寻找是否有相同的字母.
一般都是把n的长度当做滑动窗口的大小, 然后一位一位的增加, 直到窗口内容跟n一致

def str_match(target_str: str, pattern_str: str) -> bool:  
    m: int = len(target_str)
    n: int = len(pattern_str)  
    for i in range(m-n+1):#起始指针i  
        if target_str[i:i+n] == pattern_str:
            return True  
    return False  

str_match("BBC ABCDAB ABCDABCDABDE", "ABCDABD")

Sunday算法

Sunday算法跟暴力算法一样, 会先检查是否匹配, 不过在检查到不匹配后, 并不是马上移位一位, 而是根据计算来判断是否可以进行跳位, 这一步也是Sunday算法比暴力算法快点秘诀, 但是遇到像上面的BBC ABCDAB ABCDABCDABDE和ABCDABD则性能会变差, 以下是Sunday算法的流程, 以How are you和you为例子:

第一次匹配:
1
2
How are you you
发现匹配失败, 这时候就会去获取target_str字符串的第四位(因为you为3位), 发现第4位是空格, 不在you里面, 所以后面三位 ar也不可能跟you匹配, 则直接跳到are的e进行匹配.
第二次匹配:
1
2
How are you you
从e开始检查, 发现匹配仍然是失败的, 则检查target_str字符串中you的o, 发现o存在与待匹配字符串中, 只能下移一位继续匹配, 最后发现后面都you是匹配成功.

def str_match(target_str: str, pattern_str: str) -> bool:  
    m: int = len(target_str)
    n: int = len(pattern_str)  

    while i < m:
        if target_str[i: i + n] == pattern_str:
            return True
        skip_index: int = i + n
        if skip_index < m - 1 and target_str[skip_index] not in pattern_str:
            i += n * 2
        else:
            i += 1
    return False

str_match("BBC ABCDAB ABCDABCDABDE", "ABCDABD")

KMP模式匹配算法

KMP算法减少了一些已经计算过的计算量，但是他需要我们自己创建一个匹配表
对KMP算法的讲解：http://blog.csdn.net/chinwuforwork/article/details/51939826

def kmp_match(s, p):  
    m = len(s); n = len(p)  
    cur = 0#起始指针cur  
    table = partial_table(p)  
    while cur<=m-n:  
        for i in range(n):
            if s[i+cur]!=p[i]:  
                cur += max(i - table[i-1], 1)#有了部分匹配表,我们不只是单纯的1位1位往右移,可以一次移动多位  
                break  
        else:  
            return True  
    return False  
  
#部分匹配表  
def partial_table(p):  
    '''''partial_table("ABCDABD") -> [0, 0, 0, 0, 1, 2, 0]
    prefix&postfix or {''}求集合的交集，如果没有则为空
    pop()可以取出里面的数值
    '''  
    prefix = set()  
    postfix = set()  
    ret = [0]  
    for i in range(1,len(p)):  
        prefix.add(p[:i])  
        postfix = {p[j:i+1] for j in range(1,i+1)}  
        ret.append(len((prefix&postfix or {''}).pop()))  
    return ret  
  

print (partial_table("ABCDABD")  )
print (kmp_match("BBC ABCDAB ABCDABCDABDE", "ABCDABD")  )

图的最小生成树

在一个有权的图中，既要做到遍历到所有点，同时要保证遍历顺序的权加起来是最小的

普里姆算法

普里姆算法的基本思想：普里姆算法是另一种构造最小生成树的算法，它是按逐个将顶点连通的方式来构造最小生成树的

从连通网络 N = { V, E }中的某一顶点 u0 出发，选择与它关联的具有最小权值的边(u0, v)，将其顶点加入到生成树的顶点集合U中。以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(u, v),把该边加入到生成树的边集TE中，把它的顶点加入到集合U中。如此重复执行，直到网络中的所有顶点都加入到生成树顶点集合U中为止。

普利母算法过程

def prim( graph, vertex_num ):  
      
    INF      = 1 << 10  
    visit    = [False] * vertex_num   #检测是否遍历过
    dist     = [INF] * vertex_num     #该集合是用于记录且判断权的最小值（需要与visit一起判断）
    #利用dist可以做到，假如到了某个点，哪个点已经没有可以遍历的点了，就可以回到之前记录的点的没记录粿点的最小权
    my_list = []

    for i in range( vertex_num ):  
          
        minDist = INF + 1  
        nextIndex = -1  
          
        for j in range( vertex_num ):  
            #查找第i个点与未遍历的点的最小权值的对应点
            if dist[j] < minDist and not visit[j]:  
                    minDist = dist[j]  
                    nextIndex = j

        for j,n in enumerate(graph[nextIndex]):
            #查找该点的前驱
            if minDist == INF:
                a = 0
            elif n == minDist:
                a = j+1

        #记录改点(poin_list的第一个为前驱，第二个为点)
        poin_list = [a,nextIndex+1]
        my_list.append(poin_list)   
        visit[nextIndex] = True  
          
        for j in range( vertex_num ):
            #为所查找的点附上与之对应点的权
            if dist[j] > graph[nextIndex][j] and not visit[j]:  
                dist[j] = graph[nextIndex][j]

    return my_list
  
_ = 1 << 10  
#<<的解释https://zhidao.baidu.com/question/583597339.html
#所以_是1024，代表无穷大

graph=[
    [0,6,1,5,_,_],
    [6,0,5,_,3,_],
    [1,5,0,5,6,4],
    [5,_,5,0,_,2],
    [_,3,6,_,0,6],
    [_,_,4,2,6,0],
]  
  
print(prim( graph, 6 ))

克鲁斯卡尔算法（优化版）

克鲁斯卡尔算法是一种用来寻找最小生成树的算法。在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边
找最小边很容易，判断是不是回路就让我蒙了好久（现在还蒙- -），由于判断边的两个断点的最终根节点是否相同等于判断是不是构成回路，所以可以使用并查集来解决
构建最小生成树时，还要使等级低的指向等级高的，这样可以变成线性表，查找时速度就能得到提高

关于并查集：http://blog.csdn.net/qq_34594236/article/details/51834882

#Kruskal’s Algorithm
def find(C, u):
    #输出该节点的根
    #案例中，到了边14时，查找1获得3，再查找3获得6，最后才知道1的跟是6,4一步得出4的跟是6。在这个期间，就把1的跟转换为6
    #案例中，到了边32时(25和13通过23连接了，但2指向5,1指向3指向6，并没有1指向3指向2，这个路径)
    #       由于32边才通过逐级查找，判断出2跟5的跟是6
    if C[u] != u:      #判断这个点是不是根，如果不是向顶点查找(由于做了路径压缩处理，查找很快)
        C[u] = find(C, C[u])                    
    return C[u]
 
def union(C, R, u, v):
    #将其视为平衡树，等级小的指向等级大的，如果两者等级一样，则前者指像后者。最后后者等级加1
    u, v = find(C, u), find(C, v)
    #这句if,else是由等级来判断是否需要转换跟
    if R[u] > R[v]:                             
        C[v] = u
    else:
        C[u] = v
    if R[u] == R[v]:                            #等级加1
        R[v] += 1
 
def kruskal(G):
    E = [(G[u][v],u,v) for u in G for v in G[u]] #生成的E是(边的权，边的起点，边的终点)的列表
    T = set()
    C, R = {u:u for u in G}, {u:0 for u in G}   
    # 定义的c是通过路径压缩后，点的对应的最终顶节点，也就是树的根，
    #R定义的是点的等级
    for _, u, v in sorted(E): #由于使用sorted所以排序先按权排序再按起点排序，所以这样生成的树中都是数字小的充当子节点，大的充当节点（但是在整颗树中并不是这样的）
        print("(",u,v,")")
        print("C", C)
        print("R", R)
        print("u,v", u, v)
        print("C[u],u",C[u],u)
        print("C[v],v",C[v],v)
        if find(C, u) != find(C, v):
            #如果两个段点的根不同，就代表没有构成回路
            print("录入u,v",u,v)
            T.add((u, v))
            union(C, R, u, v)
        print("------")
    return T



G = {
    1: {2:6, 3:1, 4:5},
    2: {1:6, 3:5, 5:3},
    3: {1:1, 2:5, 4:5, 5:6, 6:4},
    4: {1:5, 3:5, 6:2},
    5: {2:3, 3:6, 6:6},
    6: {3:4, 4:2, 5:6},
    }


print (list(kruskal(G)))

图的最小路径

迪杰斯特拉算法(Dijkstra)

该算法执行过程中，把途中的顶点分为两个集合，当时已知最短路径的顶点集合U，以及尚不知道最短路径的顶点集合V-U。算法执行过程中，逐步扩充已知最短路径的顶点集合，每步从顶点集合V-U中找出一个顶点（它是当时已经能确定最短路径的顶点）加入U。反复执行这样的操作，直到从找到顶点v0到其他所有顶点的最短路径。该算法能同时给出这些路径以及长度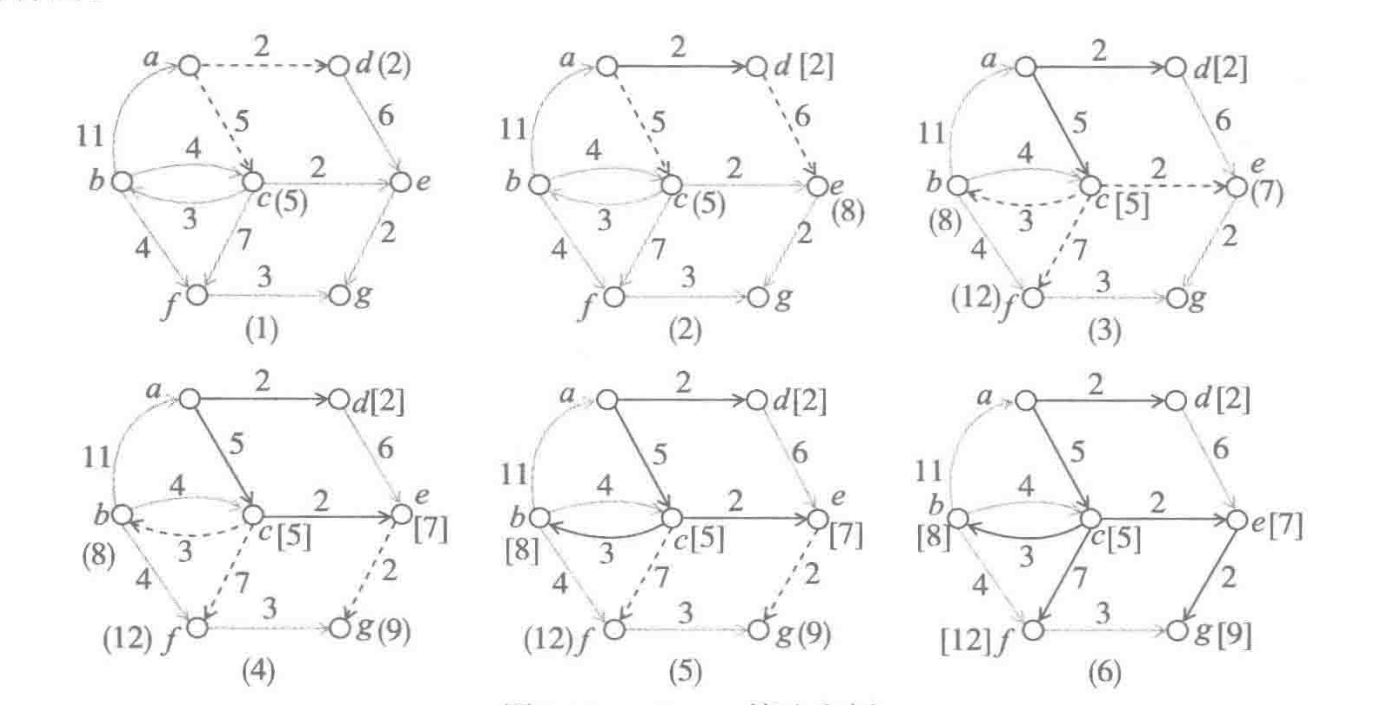
图示图
图中(1)状态，只有a在集合u，这是有两条边界变分别到顶点c和d。选择距离a最近的d加入u并标记相应的变，标出新发现的到顶点e的边界点，得到图(2)。这是最近的非u顶点是c，将其加入u后发现了3条新的边界边，找到的顶点e的新路径比原来的已知路径更短，记录这是的边界边和顶点的已知距离得到图（3）。将这是最近的非u顶点e加入集合u，记录到e的最短路径。由于新发现了从e一步可以到达g，记录相应的边界边，得到图(4)。这是虽然边界边中最短的是到g的边，但顶点b距离a更近，因此应该把b加入u。将b加入u后发现了一条到f的新路径，但其长度并不断与此时已知到f的最短路径（事实上，两条路径一样长），因此不需要更新路径，得到图（5）.再经过两步，最后状态6给出了所有路径

# dijkstra算法实现，有向图和路由的源点作为函数的输入，最短路径最为输出
def dijkstra(graph,src):
    # 判断图是否为空，如果为空直接退出
    if graph is None:
        return None
    nodes = [i for i in range(len(graph))]  # 获取图中所有节点
    visited=[]  # 表示已经路由到最短路径的节点集合
    if src in nodes:
        visited.append(src)
        nodes.remove(src)
    else:
        return None
    distance={src:0}  # 记录源节点到各个节点的距离
    for i in nodes:
        distance[i]=graph[src][i]  # 初始化
    # print(distance)
    path={src:{src:[]}}  # 记录源节点到每个节点的路径
    k=pre=src
    while nodes:
        mid_distance=float('inf')
        for v in visited:
            for d in nodes:
                new_distance = graph[src][v]+graph[v][d]
                if new_distance < mid_distance:
                    mid_distance=new_distance
                    graph[src][d]=new_distance  # 进行距离更新
                    k=d
                    pre=v
        distance[k]=mid_distance  # 最短路径
        path[src][k]=[i for i in path[src][pre]]
        path[src][k].append(k)
        # 更新两个节点集合
        visited.append(k)
        nodes.remove(k)
        print(visited,nodes)  # 输出节点的添加过程
    return distance,path
if __name__ == '__main__':
    graph_list = [ [0, 2, 1, 4, 5, 1],
            [1, 0, 4, 2, 3, 4],
            [2, 1, 0, 1, 2, 4],
            [3, 5, 2, 0, 3, 3],
            [2, 4, 3, 4, 0, 1],
            [3, 4, 7, 3, 1, 0]]

    distance,path= dijkstra(graph_list, 0)  # 查找从源点0开始带其他节点的最短路径
    print(distance,path)

沸洛伊德算法

如果我要求顶点A到顶点B之间的距离的话，我可以先找一个顶点C，求解顶点A到顶点C加上顶点C到顶点B的距离和，如何这个距离和小于顶点A直接到顶点B的距离的话，那么这个时候就要更新一下距离矩阵中的值，将顶点A到顶点B的距离更新为：顶点A到顶点C加上顶点C到顶点B的距离和。这就是Folyd的核心思想了，那么如果要找到全局最优的解就要在选取中间顶点的过程中遍历所有的节点才行

def make_mat(m, n, fill=None):
    mat = []
    for i in range(m):
        mat.append([fill] * n)
    return mat

def get_edges(graph):
    n = len(graph)
    edges = []
    for i in range(n):
        for j in range(n):
            if graph[i][j] != 0:
                edges.append((i, j, graph[i][j]))
    return edges

def ford(graph, v0):
    n = len(graph)
    edges = get_edges(graph)
    dis = [INF] * n
    dis[v0] = 0
    path = [0] * n

    for k in range(n-1):
        for edge in edges:
            # relax
            if dis[edge[0]] + edge[2] < dis[edge[1]]:
                dis[edge[1]] = dis[edge[0]] + edge[2]
                path[edge[1]] = edge[0]

    # check negative loop
    flag = False
    for edge in edges:
        # try to relax
        if dis[edge[0]] + edge[2] < dis[edge[1]]:
            flag = True
            break
    if flag:
        return False
    return dis, path
if __name__ == '__main__':
    INF = 1e6
    graph_list = [ [0, 2, 1, 4, 5, 1],
            [1, 0, 4, 2, 3, 4],
            [2, 1, 0, 1, 2, 4],
            [3, 5, 2, 0, 3, 3],
            [2, 4, 3, 4, 0, 1],
            [3, 4, 7, 3, 1, 0]]

    distance,path= ford(graph_list, 0)  # 查找从源点0开始带其他节点的最短路径
    print(distance,path)

图的拓扑排序

拓扑排序算法

拓扑顺序就是：每次找到一个只指向别人的点 (学术性说法：入度为0)，记录下来；然后忽略掉这个点和它所指出去的线，再找到下一个只指向别人的点，记录下来，直到剩最后一个点，所有记录的点的顺序就是拓扑顺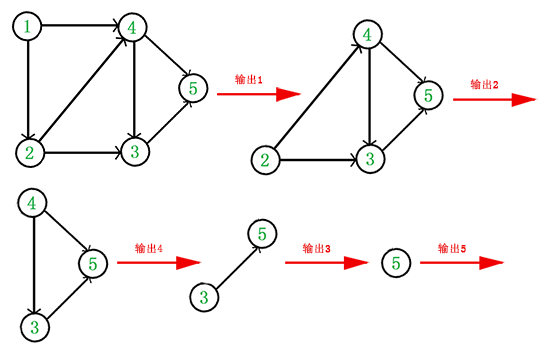序
拓扑排序
上图中，只有点1只指向别人，输出1；去掉点1和它伸出的两根线外只有点2只指向别人，输出2；…类推下去，得到拓扑排序结构: 1 2 4 3 5

def indegree0(v,e): 
    if v==[]:
        return None
    tmp=v[:]
    for i in e:
        if i[1] in tmp:
            tmp.remove(i[1])
    if tmp==[]:
        return -1

    for t in tmp:
        for i in range(len(e)):
            if t in e[i]:
                e[i]='toDel' #占位，之后删掉
    if e:
        eset=set(e)
        eset.remove('toDel')
        e[:]=list(eset)
    if v:
        for t in tmp:
            v.remove(t)
    return tmp

def topoSort(v,e):
    result=[]
    while True:
        nodes=indegree0(v,e)
        if nodes==None:
            break
        if nodes==-1:
            print('there\'s a circle.')
            return None
        result.extend(nodes)
    return result

v=['a','b','c','d','e']
e=[('a','b'),('a','d'),('b','c'),('d','c'),('d','e'),('e','c')]
res=topoSort(v,e)
print(res)

图的关键路径

关键路径算法

关键路径：在AOE网中，从始点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）的路径称为关键路径。

关键活动：关键路径上的活动称为关键活动。关键活动：e[i]=l[i]的活动

　　由于AOE网中的某些活动能够同时进行，故完成整个工程所必须花费的时间应该为始点到终点的最大路径长度。关键路径长度是整个工程所需的最短工期。

class Pro:  
    def __init__(self,pro_id,require_time,previous,pro_list):  
        self.pro_id = pro_id  
        self.require_time = require_time  
        self.previous = previous  
        #self.status = False  
        pro_list.append(self)  
  
    # def Test(self):  
    #   for item in self.previous:  
    #       if pro_list[item].status == False:  
    #           return False  
    #   return True  
    def ShowSelf(self):  
        print (self.id,self.require_time,self.previous)#self.status,  
    # def Pro_Finish(self):  
    #   self.status = True  
    def run(self):  
        total = 0  
        tmp = []  
        if self.pro_id == 0:  
            return 0  
        a = len(self.previous)  
        for x in range(a):  
            tmp.append(pro_list[self.previous[x]].run() + self.require_time)  
        print (tmp) 
        total = max(tmp)  
        print (total)  
        return total  
  
  
  
  
pro_list = []  
pro_0 = Pro(0, 0, [0], pro_list)  
# pro_0.status = True  
  
#init the pro_list  
pro_1 = Pro(1, 4, [0], pro_list)  
pro_2 = Pro(2, 3, [1], pro_list)  
pro_3 = Pro(3, 2, [1], pro_list)  
pro_4 = Pro(4, 5, [2], pro_list)  
pro_5 = Pro(5, 3, [3,4,8], pro_list)  
pro_6 = Pro(6, 1, [4], pro_list)  
pro_7 = Pro(7, 3, [5,6], pro_list)  
pro_8 = Pro(8, 5, [1], pro_list)  
pro_9 = Pro(9, 4, [7], pro_list)  
  
  
  
total_time = pro_9.run()    #此处为总项目，也可以是单个项目  
print ("Total_time:",total_time )

本文作者：So1n
本文链接：http://so1n.me/2017/10/20/19/index.html
版权声明：本博客所有文章均采用 BY-NC-SA 许可协议，转载请注明出处！

查看评论